Frudov broj

Sviđa Vam se vest ? Objavite je na nekim od servisa ispod...

шаблоны YooTheme
шаблоны Недвижимости joomla

Details: Category: Školica Plovidbe; Published on Tuesday, 12 June 2012 12:33; Written by Ivana; Hits: 10342

Frudov broj je bezdimenzijska veličina. Može se smatrati da je hidrodinamički ekvivalent Mahovom broju, a odražava sličnost kretanja u prostoru dodira dva fluida različite gustine. Fizički predstavlja odnos inercijalnih i gravitacionih sila.

Najznačajnija mu je upotreba za uspostavljanje sličnih uslova kretanja plovila na vodi. Dobio je ime po engleskom inženjeru, istraživaču u domenu hidrodinamike, Vilijams Frudu (Vilijams Frud).

Korišćenje fizičke veličine

Osnovne

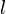$\ l$ je dužina [m]
$\ m$ je masa [kg]
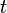$\ t$ je vreme [s]

Izvedene

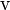${\bold \mathrm v}$ je brzina [m/s]
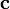$\mathbf {c}$ je generisana brzina početnog hidrodinamičkog talasa [m/s]
$\mathbf {c_w}$ je rezultujuća brzina hidrodinamičkog talasa [m/s]
$\ g$ ubrzanje zemljine teže (gravitacija) [m/s2]
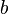$\ b$ najveća okvašena širina [m]
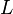$\ L$ najveća okvašena dužina [m]

Fenomen

U prirodi je rasprostranjen primer popune određenog prostora s vazduhom i vodom, to jest zajedničkog smeštaja dva fluida različite gustine. Primeri su, za slučaj voda-vazduh, mora, reke i jezera. Usled različite specifične težine vazduha i vode, pod uticajem zemljine teže, je razgraničen njihov smeštaj u prostoru. Razgraničenje predstavlja njihovu, međusobnu dodirnu površinu.

Za slučaj kretanja tela kroz prostor dodira dvaju fluida, uslovna površina tela se poklapa s dodirnom površinom fluida (u navedenom primeru, vazduha i vode). Pri kretanju se, međusobno dodirna površina fluida, menja po obliku u strujnom polju oko tela, kao na slici pri kretanju čamca.

Ovom kretanju se suprotstavlja sila, čija jedna komponenta zavisi od oblika poremećene dodirne površine fluida, u neposrednoj blizini tela.

Primeri ovakvog kretanja su plovci hidroaviona, amfibija, leteći čamac (pri poletanju i sletanju na vodu), hidrogliser, brod itd.

DEFINICIJA

Parametri talasa

U hidrodinamičkim kanalima se ispituje i meri uticaj oblika talasa na parametre kretanja tela. Talas se generiše u dodiru fluida s telom, koje se kreće po površini dodira dvaju fluida različite gustine. Na osnovu iskustva i ovakvih merenja je zaključeno da komponenta sile suprostavljanja tome kretanju, zavisi od oblika talasa, po amplitudi, periodu i učestanosti (ilustracija talasa na slici desno). Talas ima karakteristike oscilatornog kretanja, definisanog s dužinom λ m, periodom T s i s talasnom brzinom c = λ/T m/s.

Merenja se realizuju u hidrodinamičkim kanalima, za kretanje određenog tela, s razlitim brzinama i za različite veličine modela, s variranjem razmere

Bezdimenijska analiza

Imajući u vidu, da parametri talasa zavise od ubrzanja zemljine teže, te i ta komponenta sile suprostavljanja kretanju, odnosno njen bezdimenzijski koeficijent zavisi od ubrzanja g. U aerodinamici postoje isto tako primeri gde na rezultate merenja utiče zemljino ubrzanje g. To je pri ispitivanju kovita u vertikalnom aerotunelu.
Problem bezdimenijske analize je isti kao u Rejnoldsovom broju.
Hidrodinamička sila se može napisati, u prethodnom kontekstu za nestišljivo i neviskozno strujanje, kao funkcija:

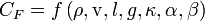
$C_F = f\left(\rho,\bold \mathrm v, l, g, \kappa,\alpha,\beta\right)$

Gde su: κ oblik aerotela, α napadni ugao i β bočni ugao.
Predhodna funkcija se može razviti u red

$C_F =\sum A \rho^x {\bold \mathrm v}^y l^z g^p \kappa^q \alpha^r \beta^s$

Primenom bezdimenzijske analize, mora se postići indentičnost dimenzija leve i desne strane jednačine:

$Dim\left[C_F\right] \equiv Dim\left[\rho^x{\bold \mathrm v}^yl^z g^p\right]$

Koeficijent hirodinamičke sile CF nema dimenziju, te i i odnos veličina na desnoj strani jednačine mora biti bez dimenzije. Znači, obe strane jednačine su bez dimenzije:

$Dim\left[C_F\right] = 1\quad\Rightarrow\quad Dim\left[\rho^x{\bold \mathrm v}^y l^z g^p\right] = 1$

Iz ovoga uslova se određuju eksponenti uticajnih fizičkih veličina, u pretpostavljenoj funkciji.

$Dim\left[C_F\right] = 1\Rightarrow l^0 m^0 t^0 \equiv \left(l^{-3} m \right)^x \left(l\, t^{-1} \right)^y l^z \left(l t^{-2}\right)^p \Rightarrow l^0 m^0 t^0 \equiv l^{-3x+y+z+p} m^{x} t^{-y-2p}\quad \Rightarrow$

$0 = -3x+y+z+p;\quad 0 = x;\quad 0 = y+2p$

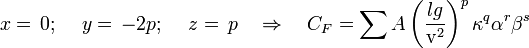
Zamenom rešenja ovog sistema jednačina, se dobija: $\,x = \,0;\quad\, y = \,-2p;\quad\, z = \,p\quad\Rightarrow\quad C_F = \sum A\left(\frac{l g}{\bold \mathrm {v^2}}\right)^p\kappa^q \alpha^r \beta^s$

Pošto su A, p, q, r i s potpuno proizvoljne vrednosti, proizilazi da je:

$C_F = f\left(\frac{l g}{\bold \mathrm {v^2}},\, \kappa,\, \alpha,\, \beta\right)$

Gde se dobijeni izraz bez dimenzije naziva Frudov broj, a označava se:

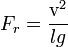
$F_r = \frac{\bold \mathrm {v^2}}{l g}$

Imajući u vidu činjenicu da je Frudov broj bez dimenzije, može se pristupiti matematičkoj postavci: $Dim\left[F_r\right] \equiv Dim\left[\frac{\bold \mathrm {v^2}}{l g}\right] = 1\quad\Rightarrow\quad\,Dim\left[F_r\right] \equiv Dim\left[\frac{\bold \mathrm {v}}\sqrt{l g}\right] = 1$

Pošto u prethodnom izrazu broioc ima dimenziju brzine (m/s), to ima i imenioc (pošto je količnik njihovih dimenzija jednak jedinici), a ima i vezu s talasom, to imenioc predstavlja talasnu brzinu, c m/s.U obrazloženju gornje funkcije CF, je naglašena činjenica da je eksponent p, nad izrazom za Frudov broj, bilo koji proizvoljan broj. Saglasno tome se može smatrati da taj proizvoljni broj u sebi sadrži i kvadratni koren, a da se pri tome ne menja smisao funkcije.Na osnovu prethodnog, može se smatrati da je Frudov broj odnos brzine tela i brzine prostiranja talasa, koji telo inicijalno generiše u fluidu (npr. u vodi)

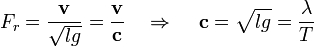
$F_r = \frac{\mathbf {v}}{\sqrt{l g}} = \frac{\mathbf{v}}{\mathbf{c}} \quad\Rightarrow\quad\,\mathbf{c} = \sqrt{l g} = \frac{\lambda}{T}$

Primena kod plovila

Za plovila:brodove, glisere, čamce itd. je Frudov broj u obliku:

$F_r = \frac{\mathbf{v}}{\sqrt{gL}}$

Gde je L usvojena najveća dužina okvašenog dela plovila, u liniji dodira vazduha i vode.
Npr. brod, pri kretanju, generiše talase s približnom talasnom dužinom kao i vrednost za L.
Teoretski gledano, strujanje oko broda se deli na kategorije:

pod-kritično Fr<1, brzina broda je manja od brzine raspostiranja talasa
kritično Fr=1, brzina broda je jednaka brzini rasprostiranja talasa
nad-kritično Fr>1, brzina broda je veća od brzine rasprostiranja talasa

U grupu podkritičnih strujanja spadaju velike brzine brodova koji plove u dubokim vodama, gde se neometano razvijaju divergentni talasi.
Kroz kritični režimi strujanja su u opsegu Frudovih brojeva:

$F_r = 0,85\div 1,1$

Rezultujući talas se prostire rezultujućom brzinom od

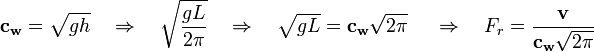
$\mathbf {c_w} = \sqrt{g h}\quad\Rightarrow\quad\sqrt{\frac{g L}{2 \pi}}\quad\Rightarrow\quad \sqrt{g L} = {\mathbf {c_{w}}} \sqrt{2 \pi}\ \quad\Rightarrow\quad F_r = \frac{\mathbf{v}}{\mathbf {c_{w}}\sqrt{2 \pi}}$

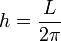
Gde je: $h = \frac{L}{2\pi}$

U slučaju izjednačenja

$\mathbf \mathbf{v} = \mathbf{c_w}\quad\Rightarrow\quad F_r = \frac{1}\sqrt{2 \pi}\quad\Rightarrow\quad F_r \approx 0,4$

Kada brzina broda pretekne vrednost 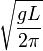$\sqrt{\frac{g L}{2 \pi}}$ , onda pretiče i brzinu rezultujućeg talasa i počinje da glisira. U tome slučaju je Frudov broj:

$F_r \geqq 0,4$

Tada brod glisira na površini vode, uporedivo kao i avion kada leti nadzvučnom brzinom.

Pri ovim uslovima, naglo opadne sila otpora od talasa, koja se suprotstavlja kretanju plovila. Kod aviona je inverzni slučaj, otpor naglo poraste u nadzvučnom letu.To je sasvim objašnjivo, s jasnom argumentacijom fizikalnosti. U nadzvučnom letu je avion izložen uticaju snažnih udarnih talasa, a posledično i skoku otpora.Plovilo pri glisiranju se oslobađa od talasa vode i od njihovog izazivanja komponente sile otpora. Otpor, kretanju plovila se svodi, samo na komponente sile otpora od vazduha i od trenja usled glisiranja po površini vode.

Da bi se glisiranje ranije izazvalo i podržalo, na hidrogliser se ugrađuju hidrokrila, s kojima se stvara hidrouzgon i plovilo se podiže u poziciju glisiranja, još na manjim brizinama. Ova se tehnologija redovno koristi kod hidroglisera za brže i lakše uspostvljanje režima glisiranja.Frudov broj je koristan za upoređenje i analizu uticaja veličine trupa na otpor broda.

Talasi u plitkoj vodi

Za talase u plitkoj vodi, kao što su talasi plime, prelivi preko brana i vodopada je Frudov broj:

$F_r = \frac{\mathbf{v}}{\sqrt{g d}}$

Gde je d širina poprečnog preseka strujnog polja, na koji je tok uprošćeno sveden.

Ovde se isto za vrednosti Frudovog broja Fr < 1 se koristi naziv pod-kritični protok, za Fr = 1, kritični protok i Fr > 1 nad-kritični protok.

Izvor: www.wikipedia.org

Moja Lađa

Frudov broj

шаблоны YooTheme
шаблоны Недвижимости joomla

новинки кинематографа
Машинная вышивка, программа для вышивания, Разработка макета в вышивальной программе, Авторский дизайн

Moja Lađa

Frudov broj

шаблоны YooTheme шаблоны Недвижимости joomla

новинки кинематографа Машинная вышивка, программа для вышивания, Разработка макета в вышивальной программе, Авторский дизайн

шаблоны YooTheme
шаблоны Недвижимости joomla

новинки кинематографа
Машинная вышивка, программа для вышивания, Разработка макета в вышивальной программе, Авторский дизайн